[L1] Regression (Univariate). Cost Function. Hypothesis. Gradient.¶
This is the first post in a series, covering notes and key topics in Andrew Ng's seminal course on Machine Learning from Standford University, the web's most highly rated machine learning course, and content direct from one of the field's most influential contributors.
The series is a compilation of notes from my time through the course, and is in essence aimed to be a useful machine learning handbook that students can refer to or that practitioners can use as a reference for foundational review.
Machine Learning from Standford takes practitioners through a bottom-up approach introduction into the field, covering the theory and the math which underpins modern machine learning today. Topics include linear regression, classification, neural networks, and also practical information for working with machine learning models in the wild and what to look for during training.
It comes highly recommended. https://www.coursera.org/learn/machine-learning
This first post covers the basics. An introduction into what machine learning actually is, and the topics of model hypothesis, cost functions, and gradient descent.
What is Machine Learning¶
Definitions¶
ML Definition - Field of study that gives computers the ability to learn without being explicitly programmed.
ML Definition - A computer program is said to learn from experience E with respect to some task T and some performance measure P, if its performance on T, as measured by P, improves with experience E.

What is Machine Learning?

Supervised Learning

Unsupervised Learning

Note: A good rule of thumb is that supervised learning teaches machines to make predictions, while unsupervised learning teaches machines to find relationships.
Classification and Regression¶
Classification - Discrete Valued Output (ie is this email spam or not spam)
Regression - Continuous Valued Output / Real valued output
Linear Regression - Data is said to "regress" to a mean. Predicts continuous valued output.

Hypothesis¶
Hypothesis. Univariate
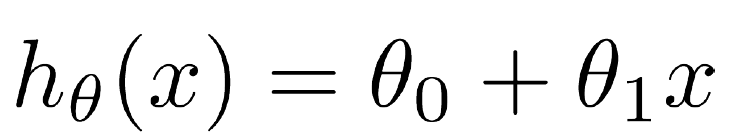
Hypothesis in Linear Regression
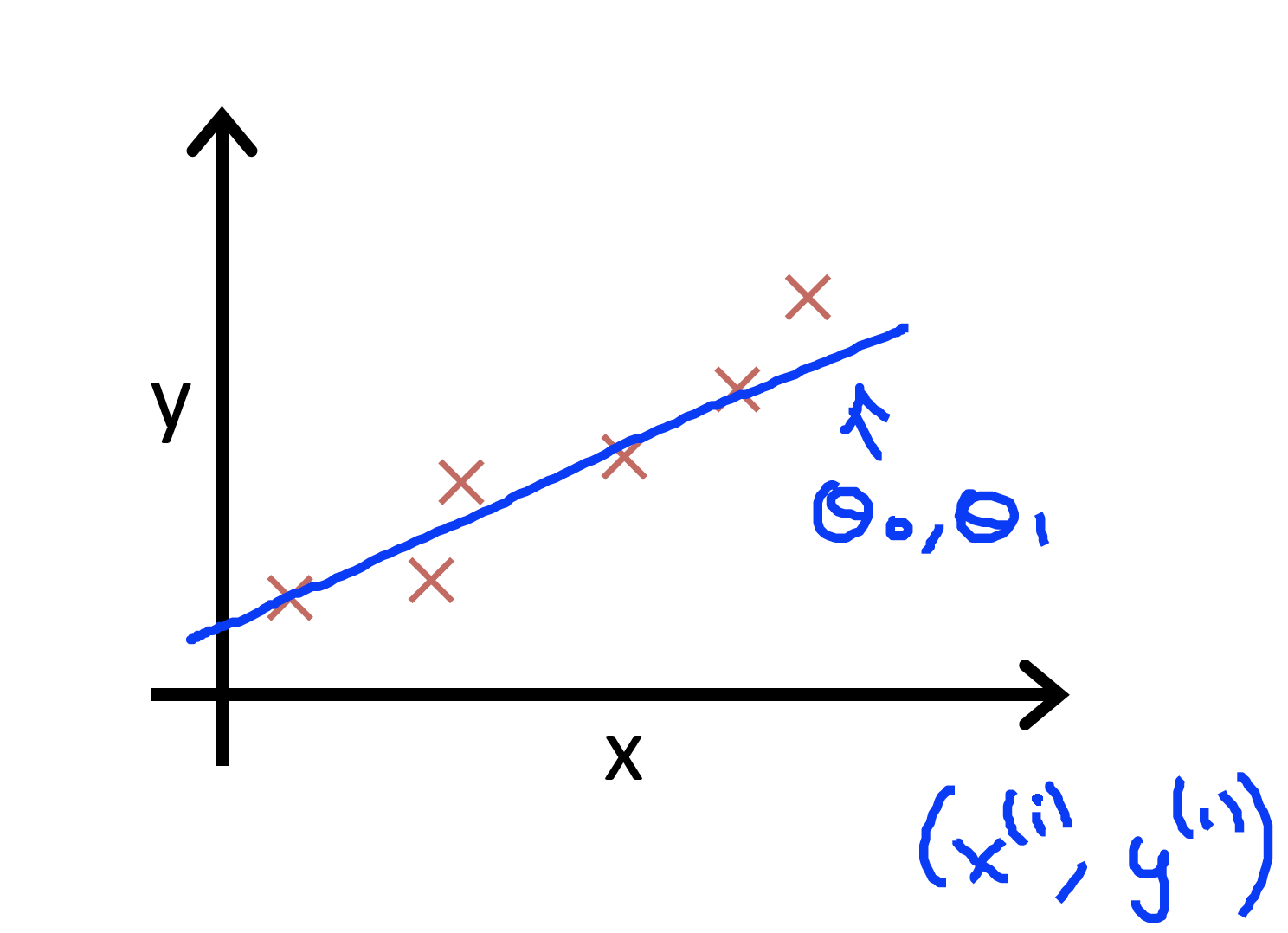
Another Example:
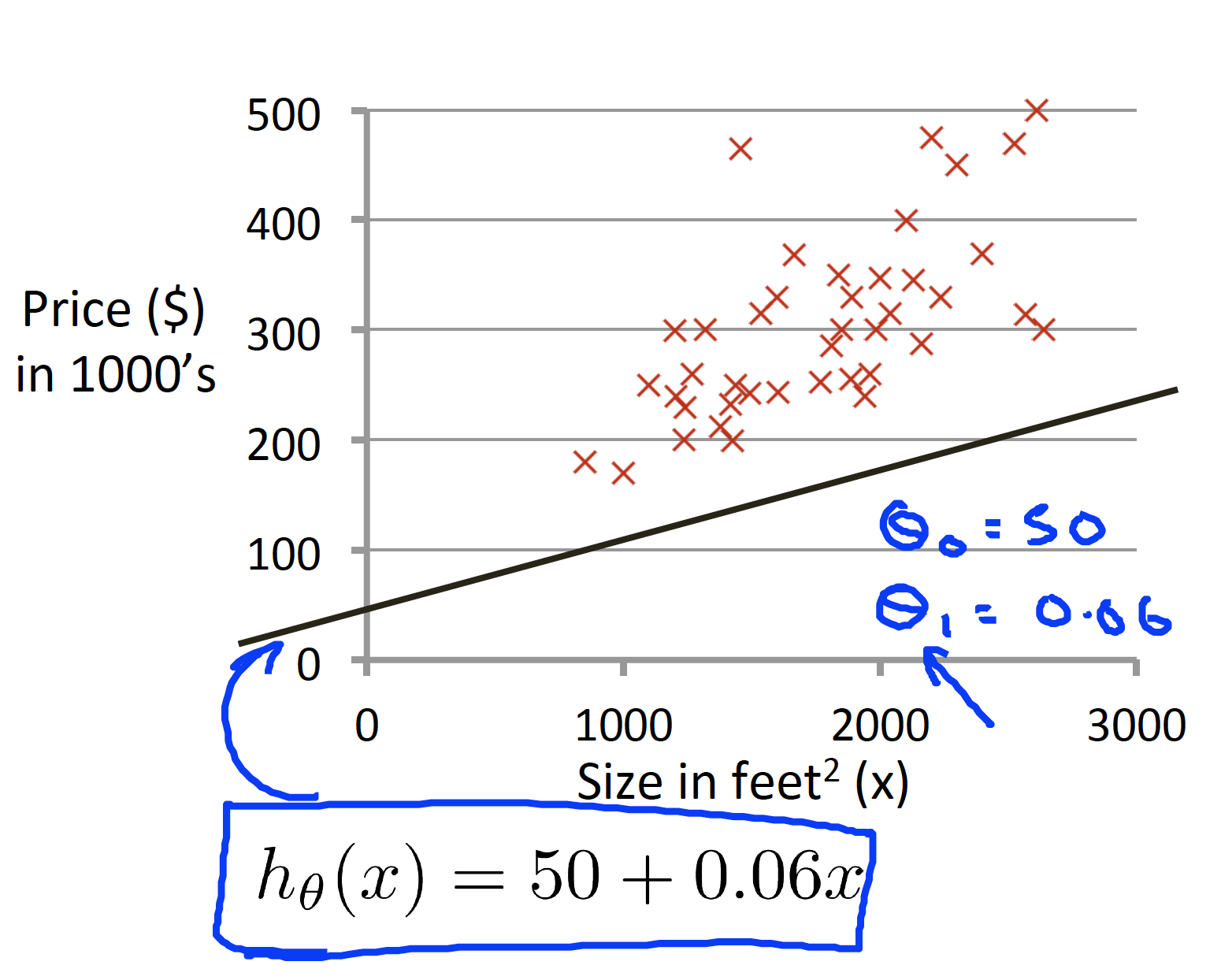
Cost Function¶
Cost Function - Average of differences between predicted values and the actual values. Also known as the "squared error".
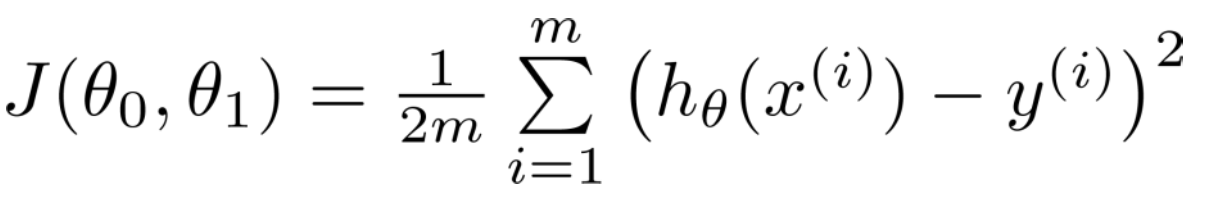
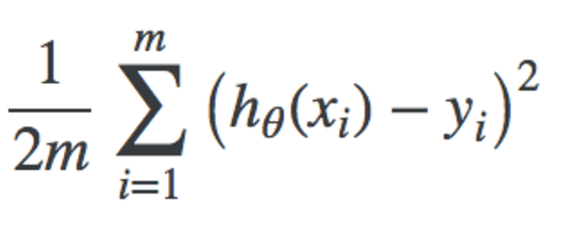
Cost function - measures the accuracy of our hypothesis function by using this.
Minimising the cost of the prediction is the goal of accurate machine learning models.
Additional Notes¶
Why does the cost function include multiplying by 1/(2m)?

In the cost function, why don't we use the absolute value, instead of the mean squared?

Cost Function Derivative¶
To prepare for the next step in gradient descent, we need to understand the derivative of the cost function.
Starting with the cost function, we can work out its derivative like this. Which leads to the following definition of the derivative of the cost function.
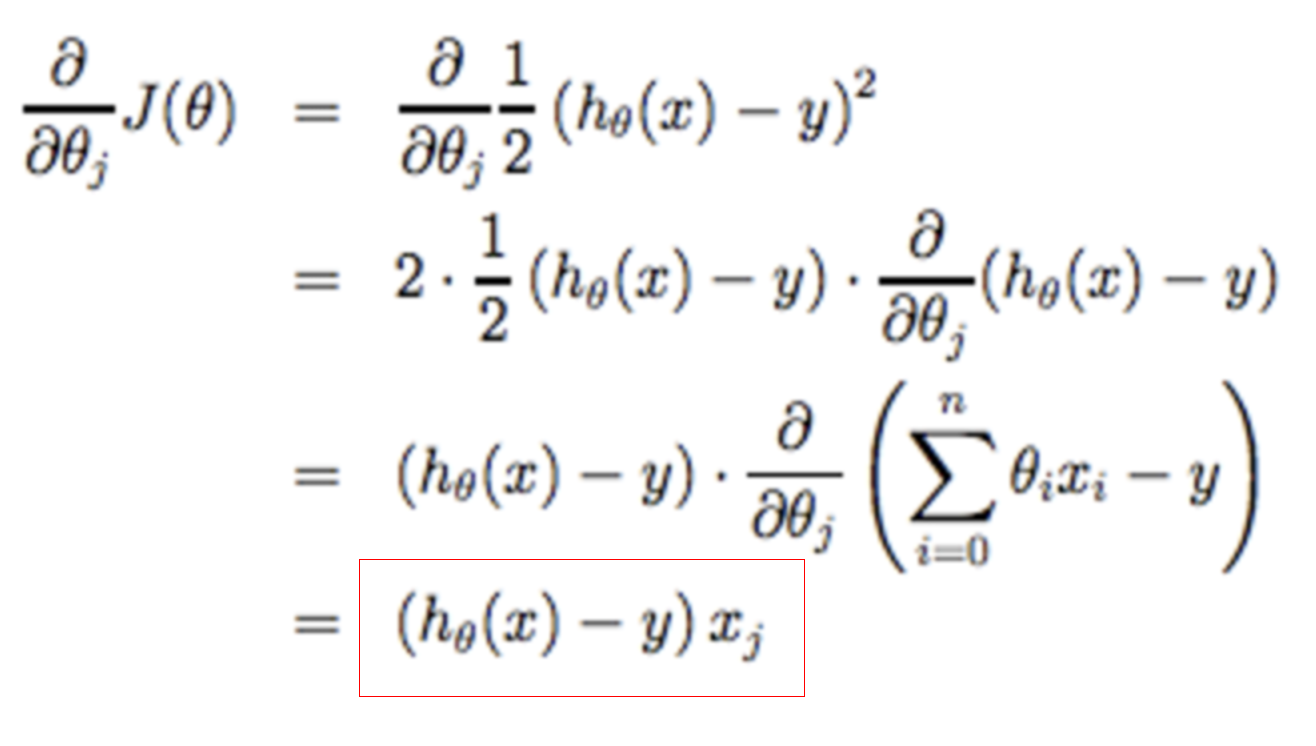
Derivative of the Cost function.
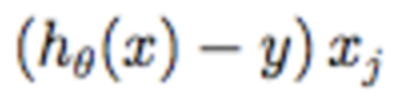
Gradient Descent¶
The general form for gradient decent.
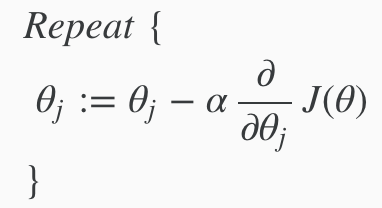
Gradient Descent is a way to minimise the cost function. We use the derivative of the cost function in the gradient descent algorithm.
Gradient descent formula for linear regression. We take theta, then subtract the derivative of the cost function that is also multiplies by a tuned alpha learning rate. We repeat this until convergence.
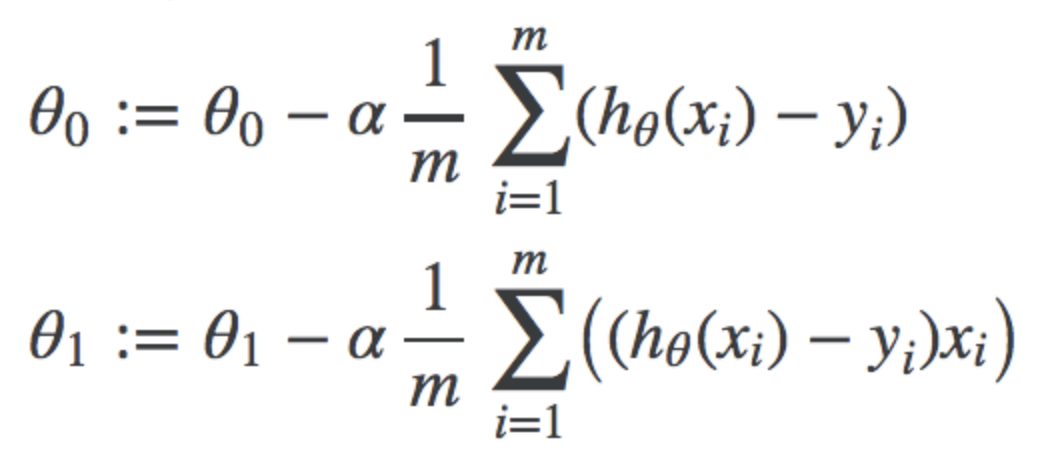
General formula for Gradient Descent using the derivative notation. Where j represents the feature index number. For univariate Linear regression, j is either 0 or 1.
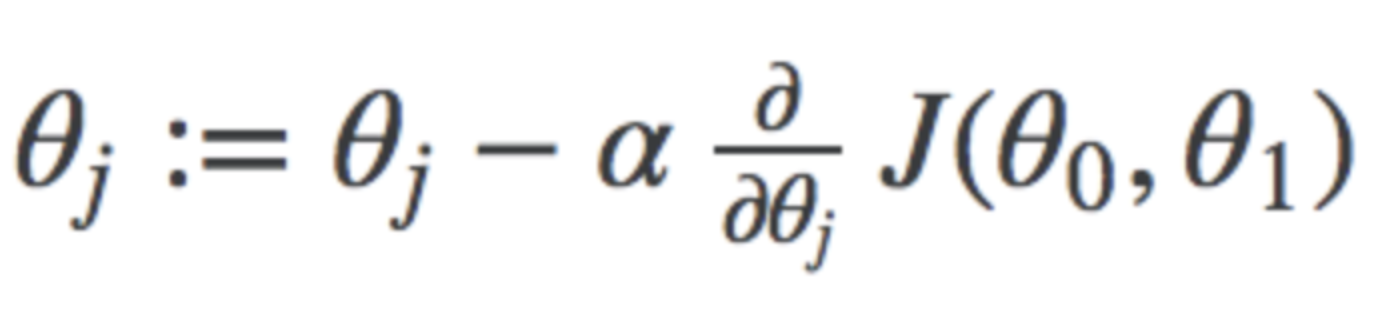
So for example, the gradient descent component for theta1 looks like this.
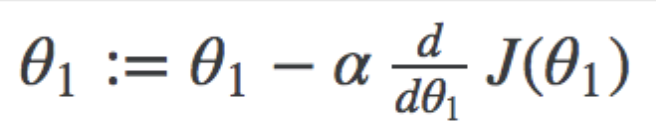
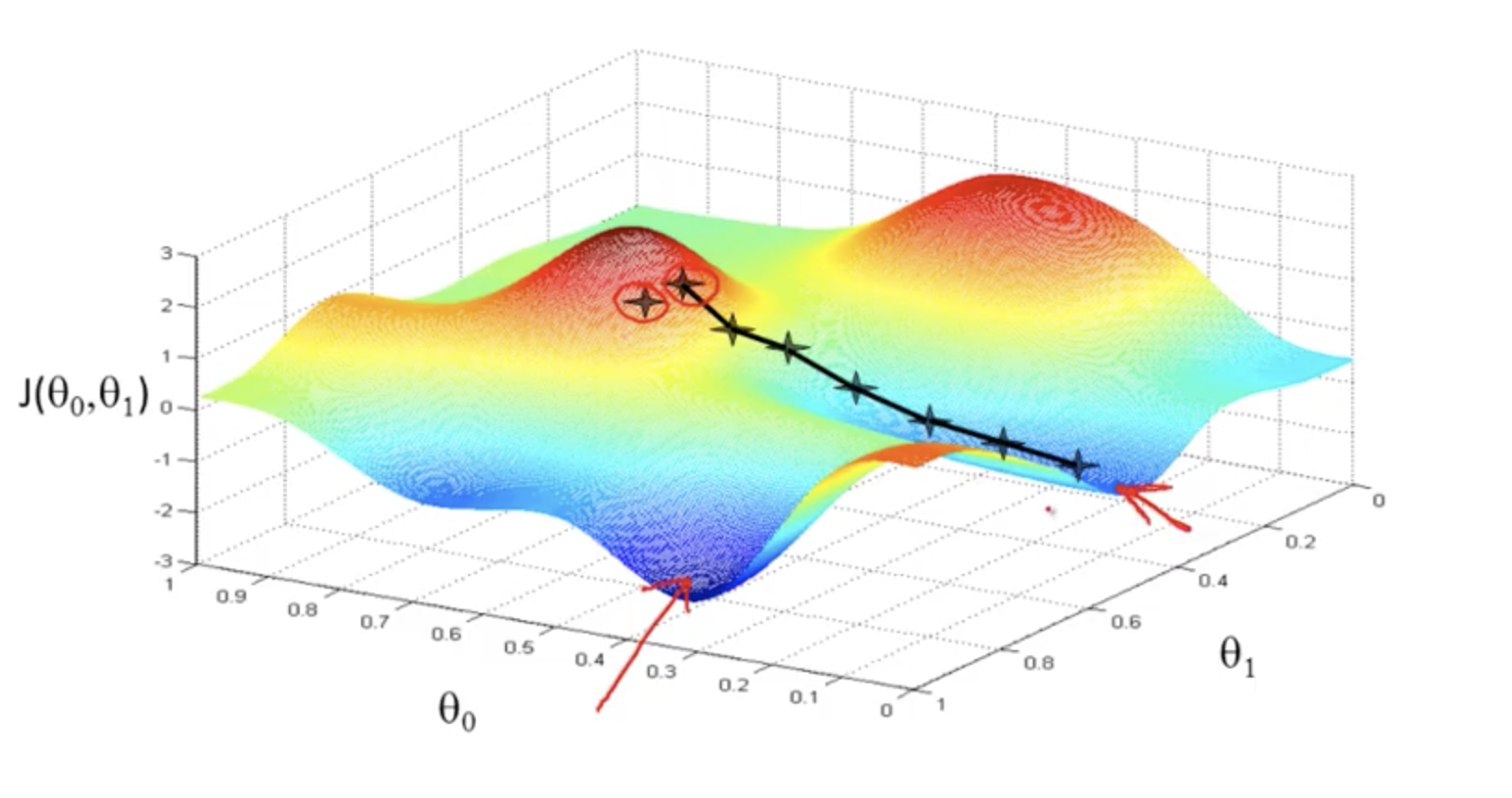
Gradient Descent. Visualised - Used to minimise the cost function.
Gradient Descent - Derivative¶
This component here of the gradient descent formula represents the derivative of the cost function. The first for theta0, the second for theta1.
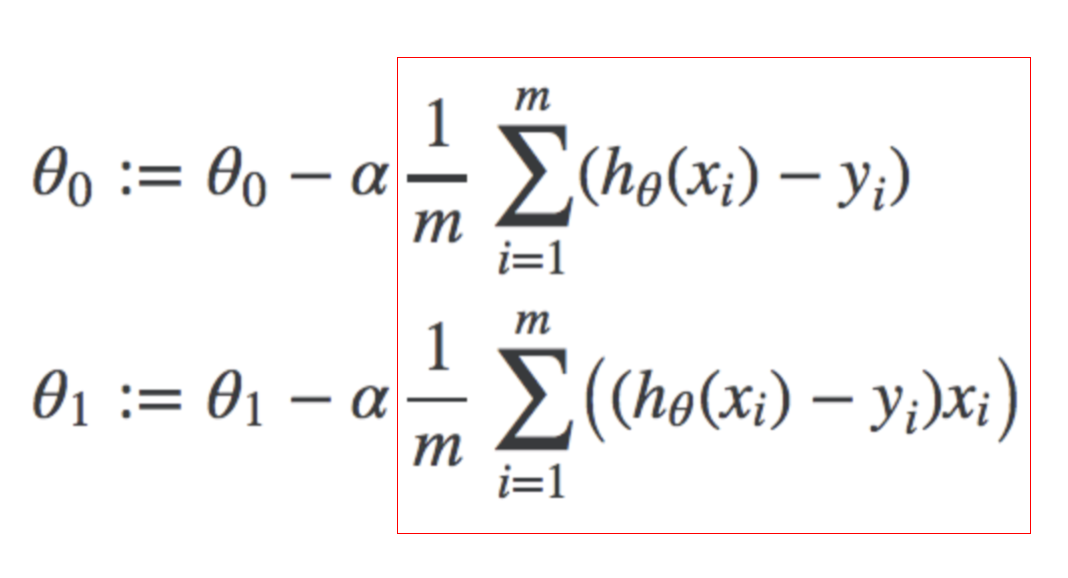
Gradient Descent - Convergence Intuition.¶
- Gradient Descent uses the derivative of the cost function J
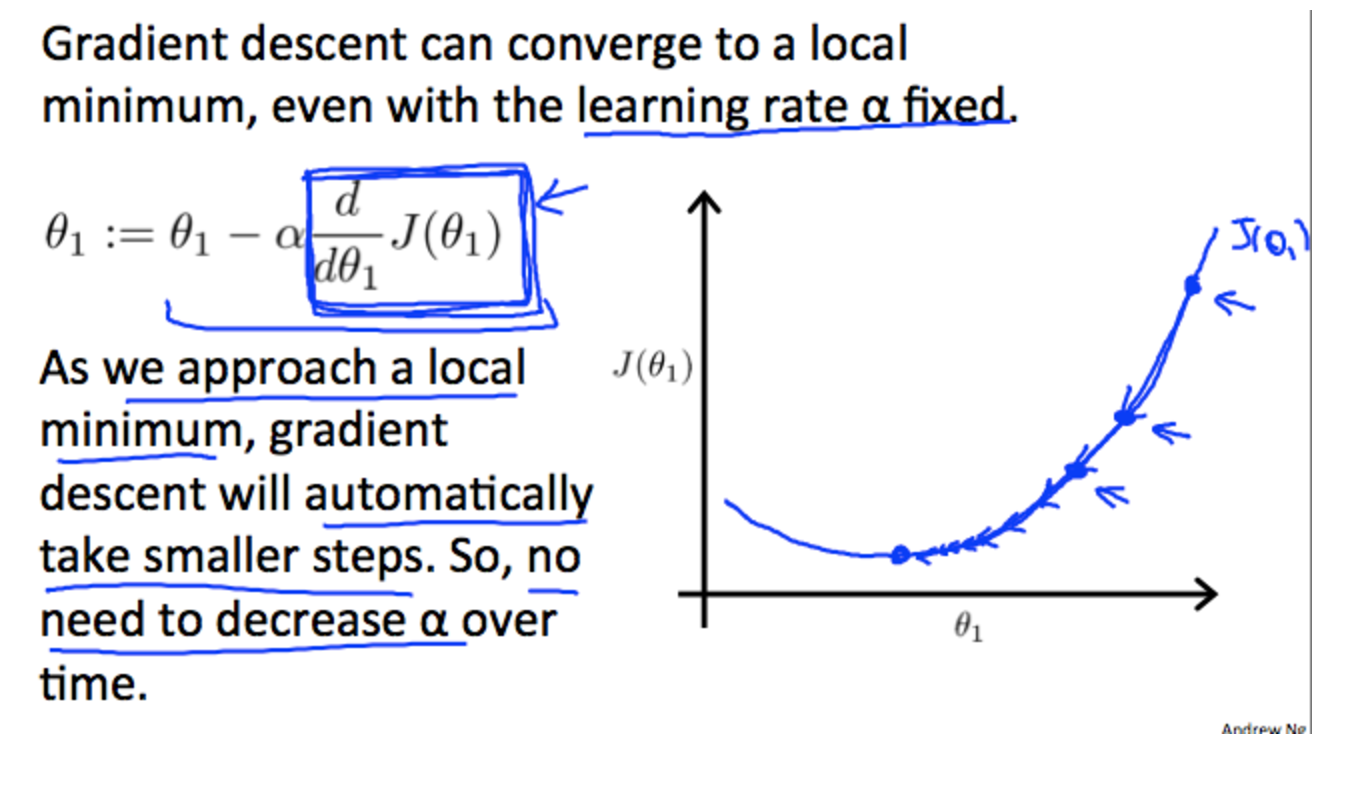
- The intuition behind gradient descent convergence is that the derivative of the cost function will approach 0 near the local minimum.
- At the minimum, Gradient descent will always be 0 (ie a flat slope line with no gradient)
- Gradient Descent can converge to a local minimum even with a fixed learning rate. So no need to change the learning rate of time.
- If the Gradient descent is already at local minimum, another step will just keep the descent at the local minimum
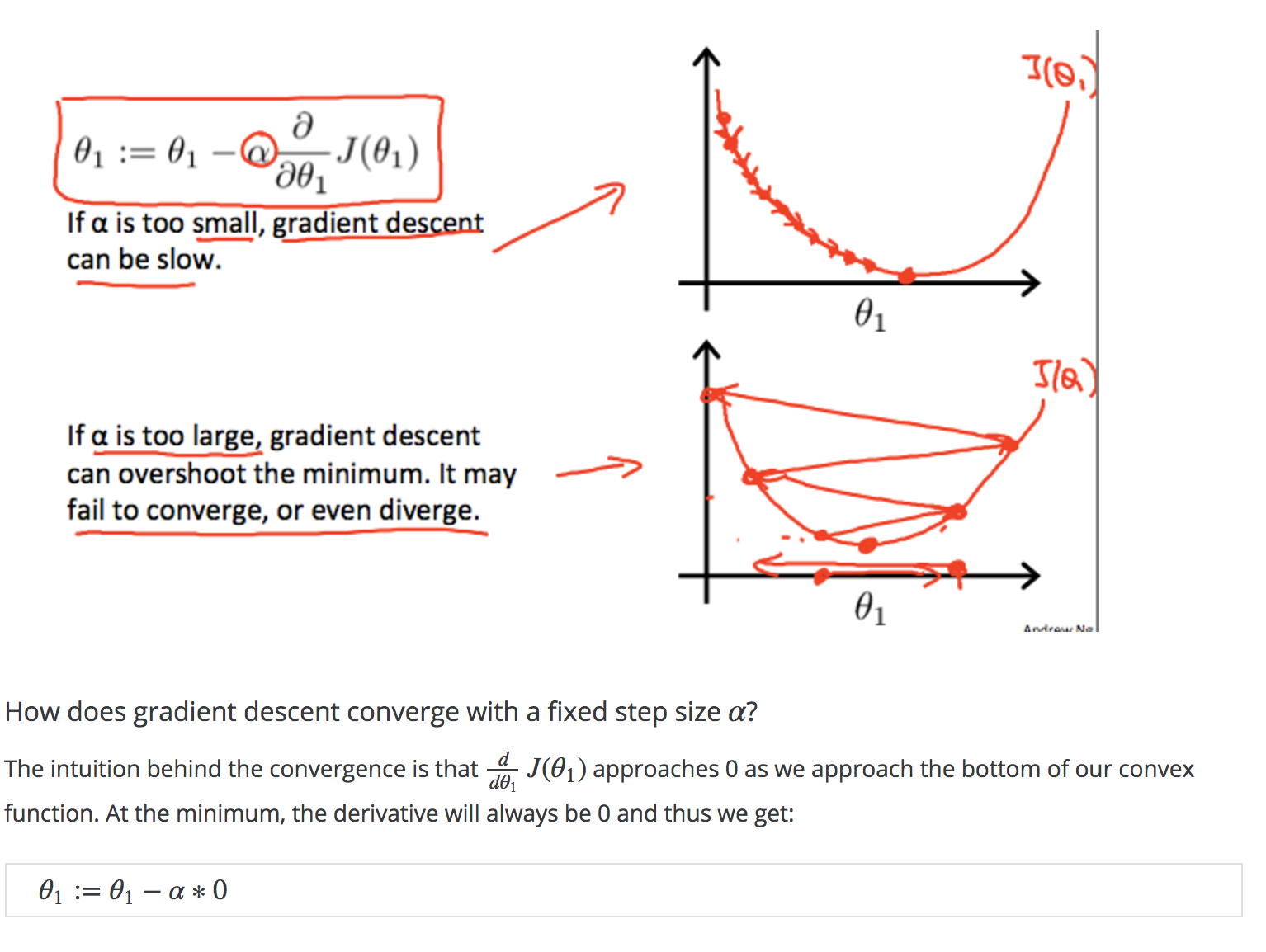
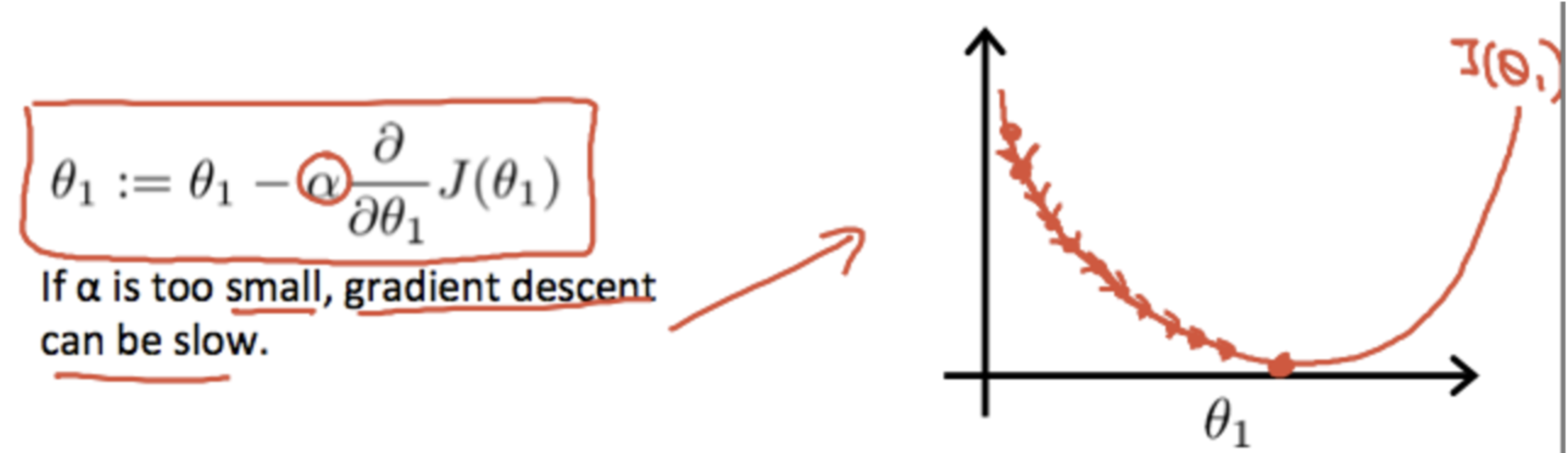
- If the learning rate alpha is too small, gradient descent can be slow.
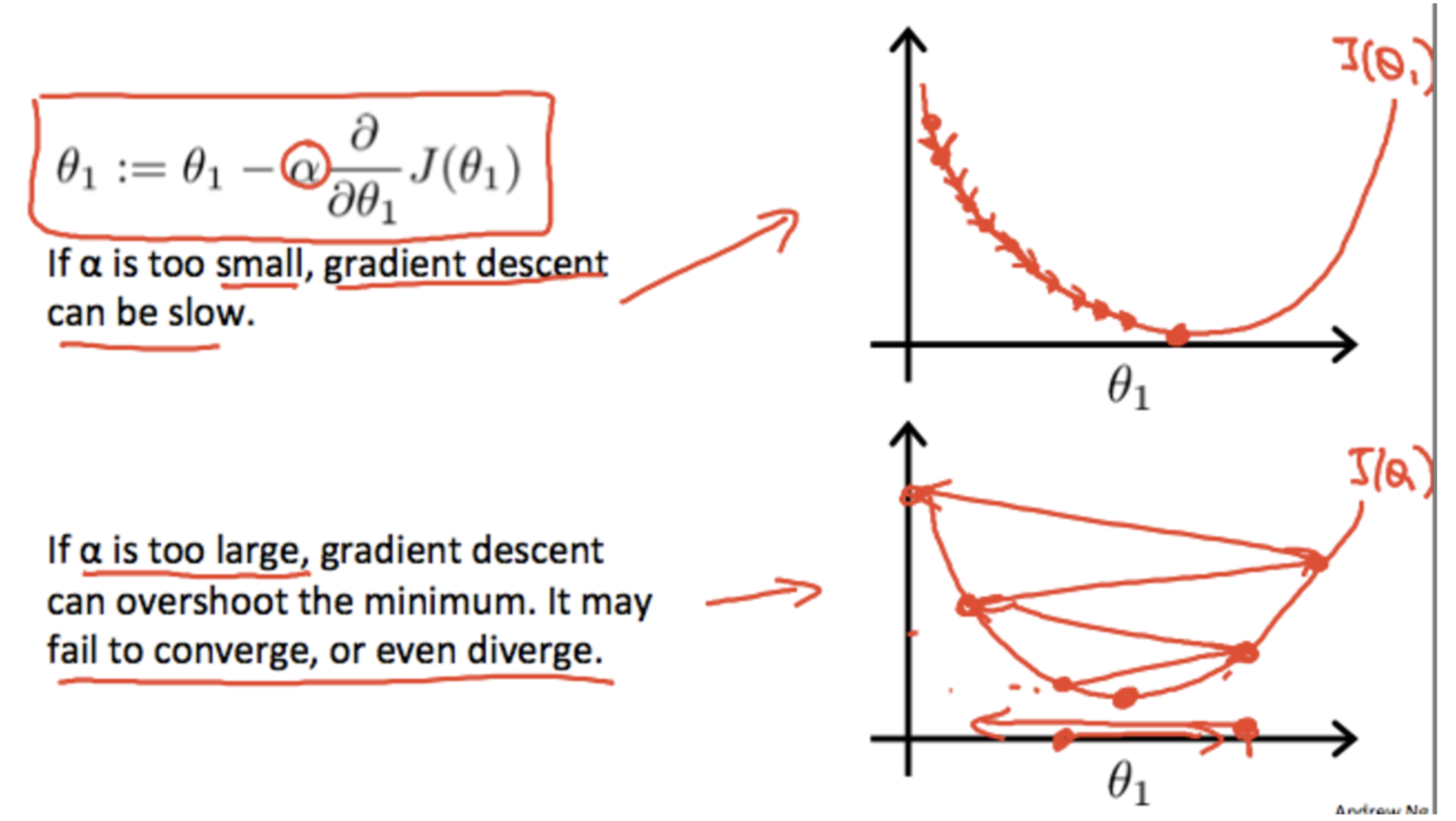
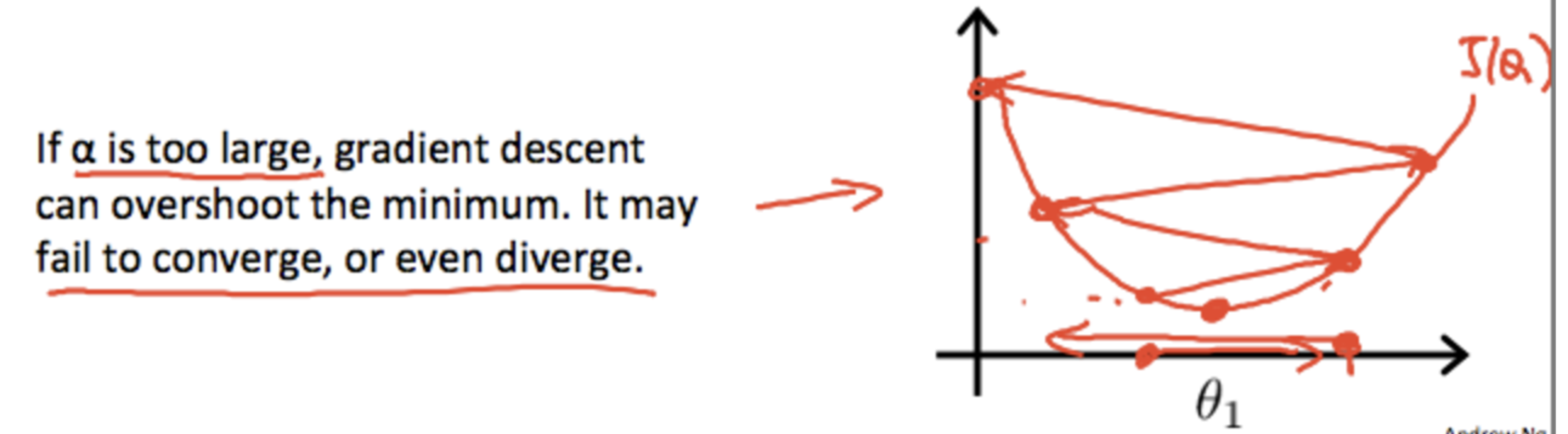
- If learning rate alpha is too large, it may not converge at all, or even diverge.
Cost Function and Gradient Descent - Visualised Intuitions¶
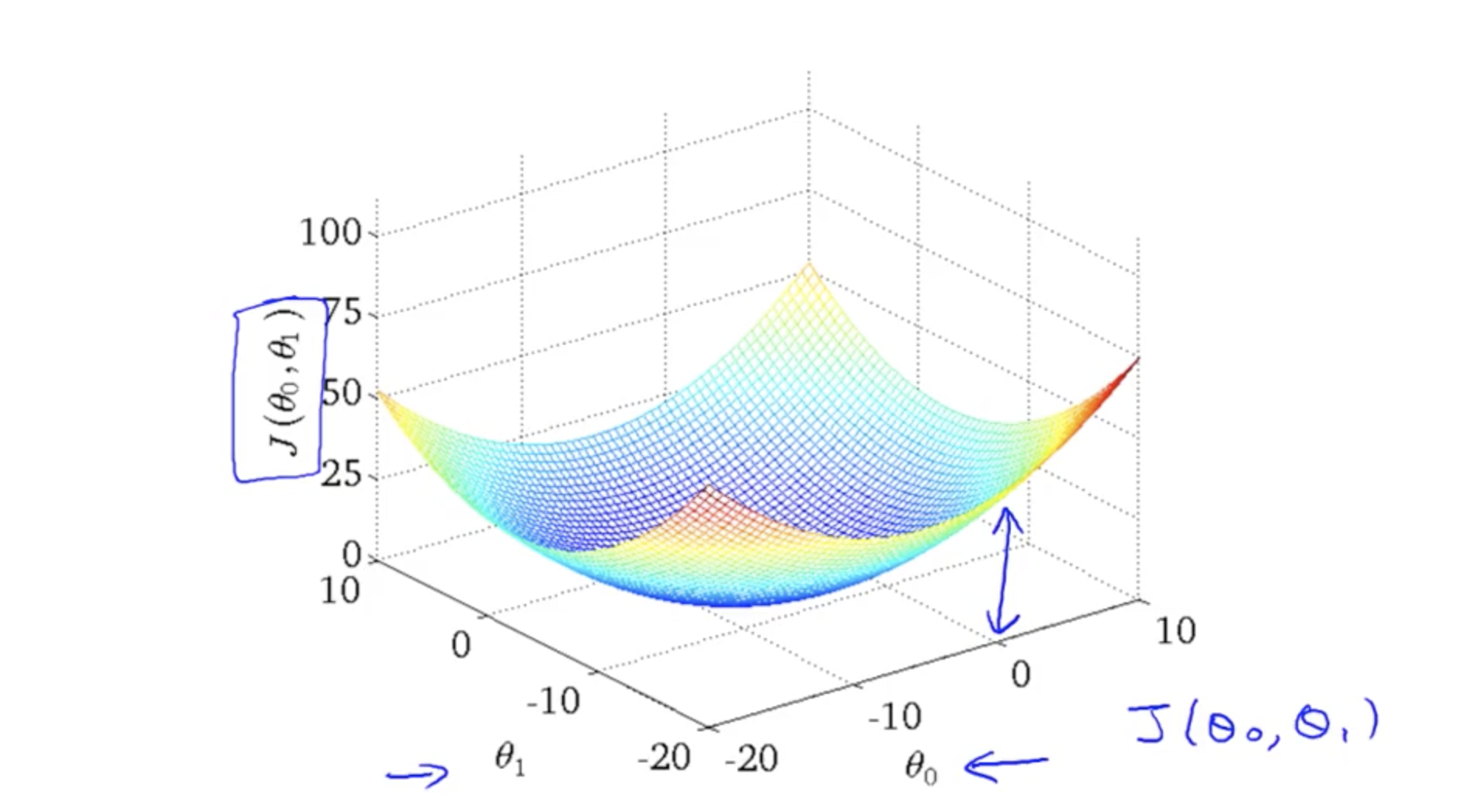
Cost Function Plotted in three dimensional space with theta0 and theta1. The bottom of the trough is still the minimised point of the cost function.
Gradient Descent. Visualised - Used to minimise the cost function
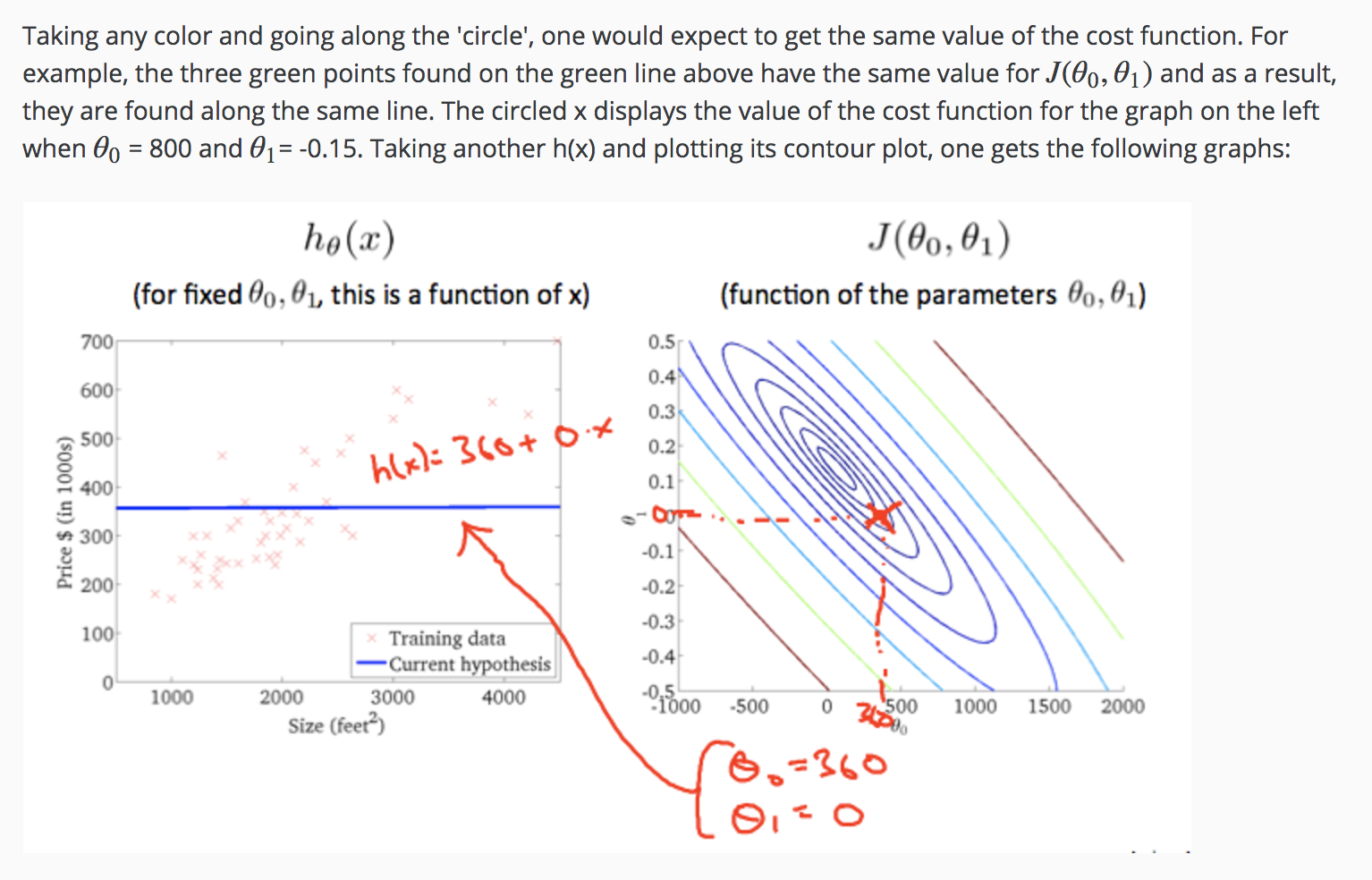
Cost Function - Contour Plot Intuitions¶
Hypothesis and Cost Function - Using Contour Plots
Contour Plot Intuition 1
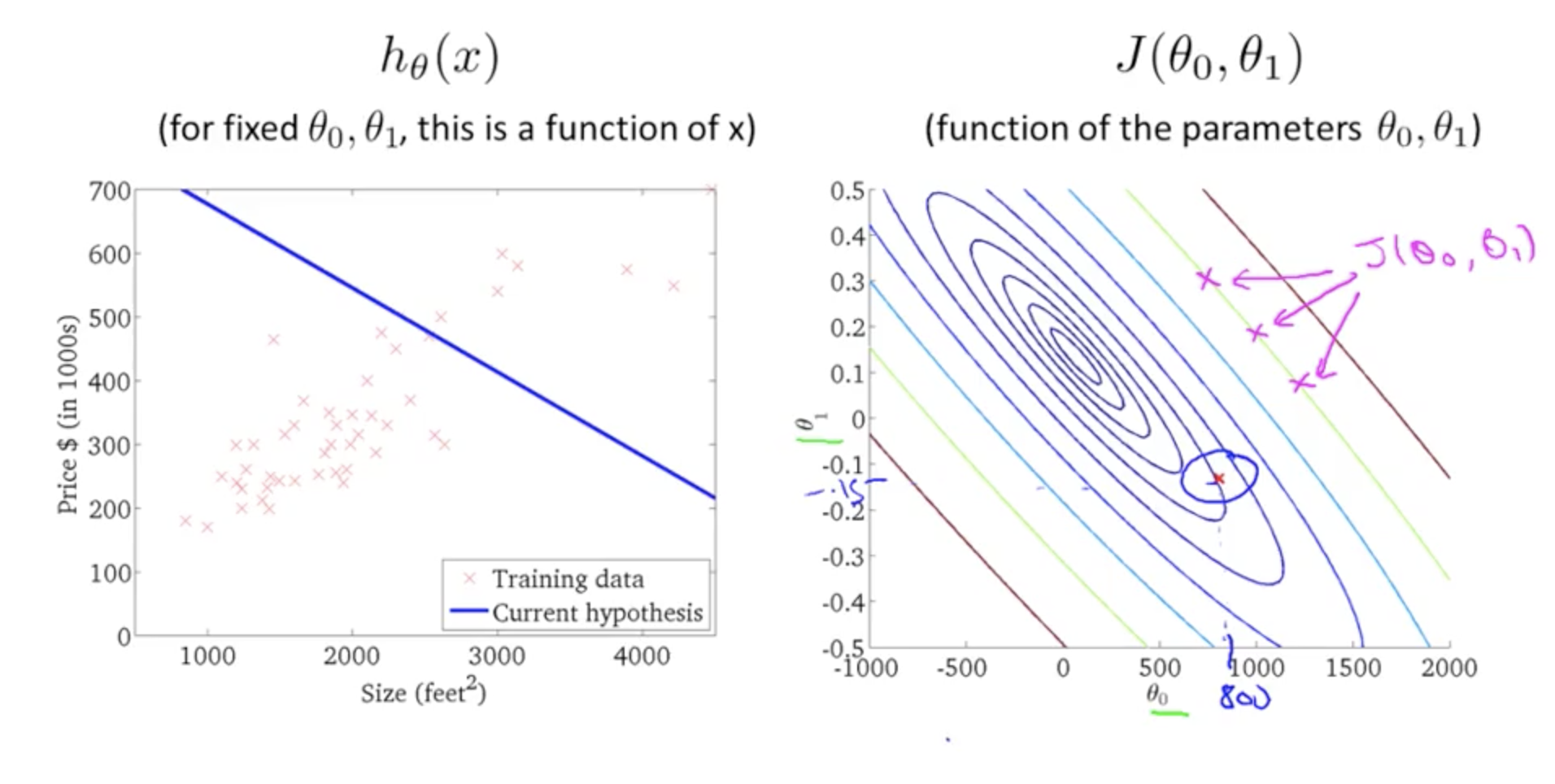
Contour Plot Intuition 2
ML Model Approach - Summary of Process¶
Overview¶
- Hypothesis
- Cost Function
- Minimising the cost (Gradient Descent).
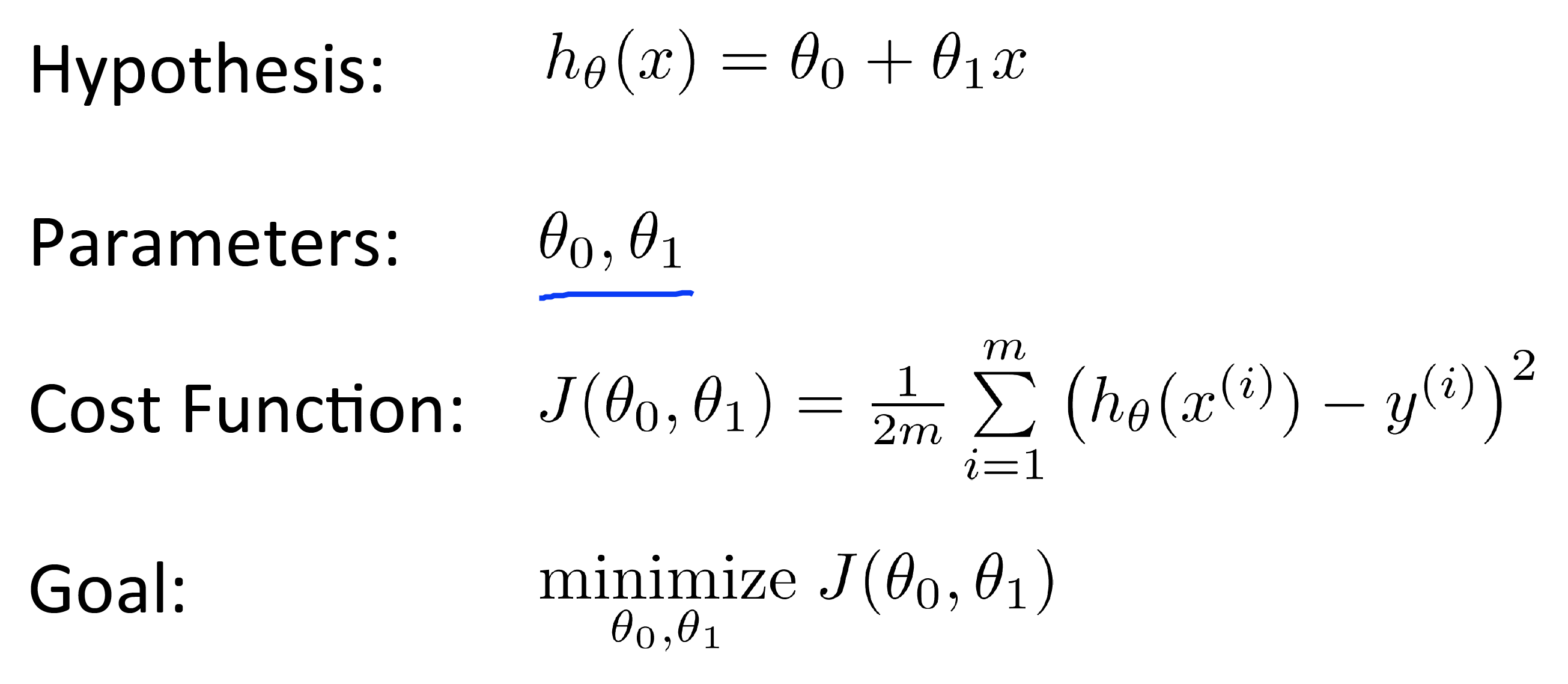
Gradient Descent Steps¶

General formula for Gradient Descent summarised.

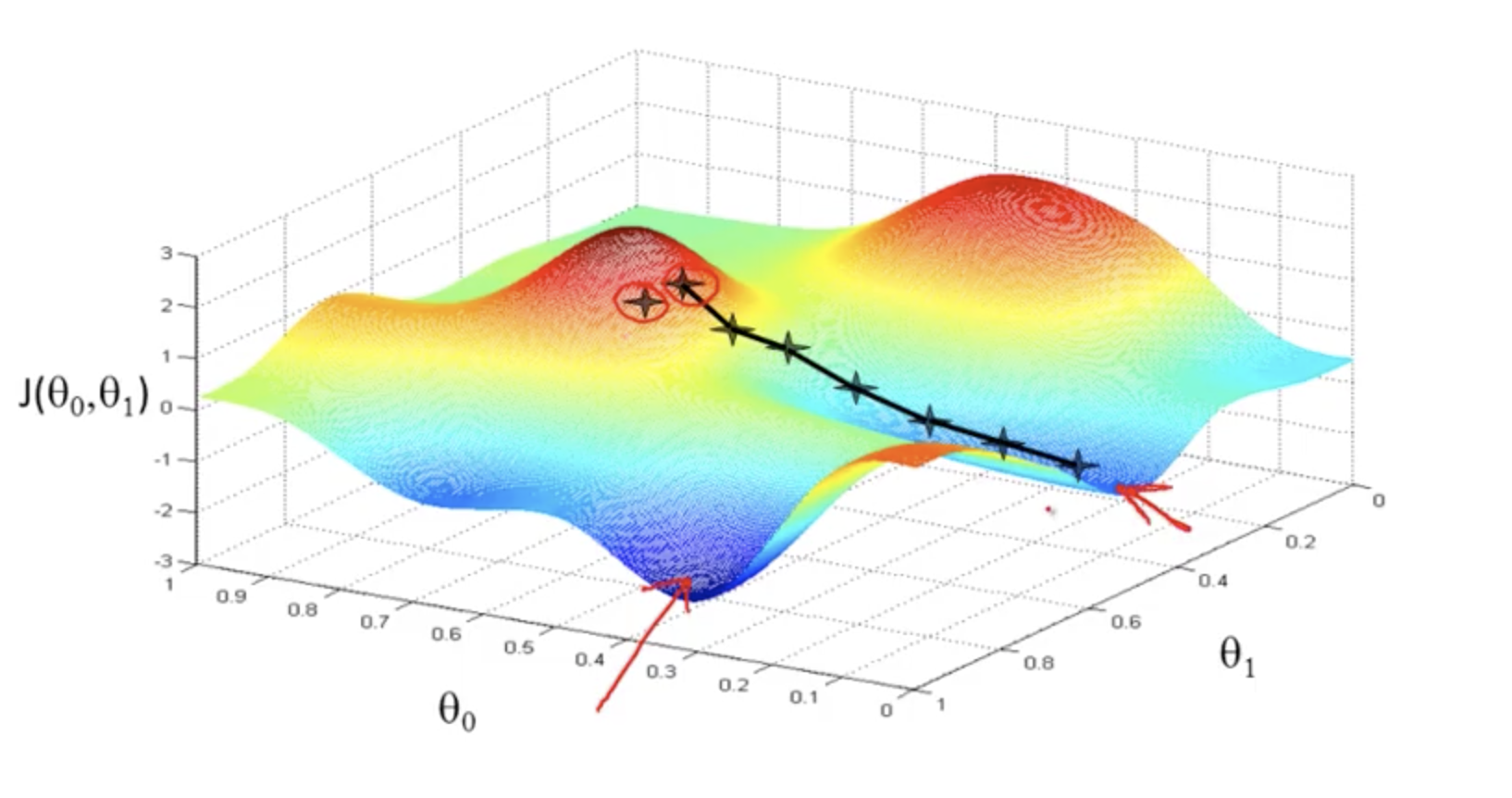
The initial values (in Cost functions where there are more than one local minima) - the initial values of gradient descent can affect which local minima you end up with